
본 포스팅은 Logic and Computer Design Fundementals (Pearson, 2013)의 내용을 다루고 있습니다.
Introduction
Logic Design 논리설계란?
단순화시켜서 이야기하면, 논리설계란 다수의 게이트들을 연결하는 것이다.
Gate
Logic Gate 게이트란?
논리 게이트는 기본 프리미티브 모듈이다.
- 게이트는 입력(들)과 출력(들)을 가진다.
- 게이트의 입력과 출력들은 이진값 0(false) 또는 1(true)를 가진다.
- 여기서 0과 1은 각각 낮은 전압과 높은 전압을 추상적으로 말하는 것
- 디지털 회로도 전기회로의 한 종류이다.

게이트의 특성을 어떻게 정의하는가?
ONEWAY - 입력과 출력의 관계를 보여준다.
일반적으로 표나 함수와 같은 수학적 방법을 사용하여 gate를 정의한다.
1. Table 표

- verbally하게 표현한다면, 출력 값과 입력 값은 반대이다.
- 임의의 어떤 게이트의 특성을 정의하기 위하여 말대신에 테이블을 써서 표현가능하다.
- 이러한 테이블들을 진리표 truth table 이라고 부른다.
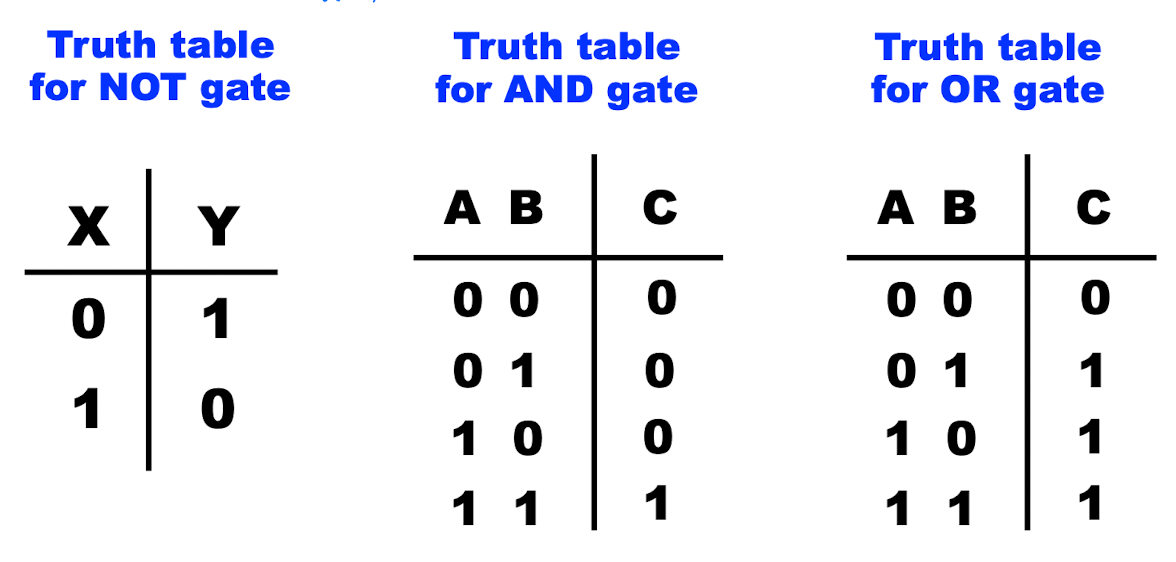
진리표를 사용하여 게이트의 특성을 나타낼 수 있다.
2. function 수학적 함수
입력과 출력의 관계를 나타내기 위하여, 특별한 수학적 연산자를 사용한다.
이를 Logic operation 논리 연산자라고 한다.

논리 연산자를 사용하여, 게이트릐 특성을 수학적 함수로 나타낼 수 있다.
Bool Algebra 부울 대수
논리 연산자는 게이트들을 특별한 수학적 함수로 정의한다.
이 특별한 수학적 함수는 부울 대수라는 특별한 대수에 기반을 둔다.
Bool Algebra

위와 같이 표현된 식은 출력값 Y에 대해 Boolean equation또는 Boolean function이다.

부울 대수에서는 위와 같은 중요한 항등식과 정리들이 있다.
15번의 distribute 법칙은 일반적인 대수의 계산과 달라 헷갈릴 수 있으므로 주의한다.
More on Gates and Boolean Algebra
자주 사용되는 로직게이트에는 NAND NOR XOR XNOR 등이 있다.

위의 사진은 각 게이트들을 스키메틱과 부울식, 진리표로 나타내었다.
논리 회로를 설계할 때에는 가장 처음으로 진리표로 회로를 정의하고, 부울 함수로 바꾸어 표현한 뒤, 마지막으로 스키메틱으로 표현할 수 있다.
진리표에서 부울식으로 나타내었을 때, 우리는 이를 optimize 최소화 할 수 있다.

Logic Expression
우리는 A와 B를 입력값으로, C를 출력값으로 가지는 임의의 게이트가 있다고 하자.
이 로직게이트의 특성을 정의하기 위해서는 모든 경우의 수를 진리표로 나타내야 할 것이다.

우리는 이러한 C출력값의 경우의 수들 중 1가지 case에 대해 true를 띄는 출력값을 찾아 볼 수 있다.
이는 C1 C2 C4 C8 이며 이를 minterm이라고 부른다.
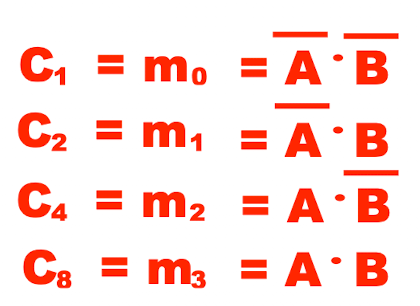
다른 출력값들은 이러한 minterms m0,m1,m2,m3의 sum로 표현될 수 있다.
용어 정의
- Literal
: 입력변수 그 자체(A, B, etc)이거나, 또는 그것의 complement(^A, ^B, etc)이다. - Product (적항)
: 적항은 1개 이상의 리터럴들이 AND 연산자로 묶여진 것인데, 단 입력변수 X와 그것의 보수 ^X가 동시에 존재하지는 말아야 함. - Minterm (최소적항)
: 최소적항은 모든 입력들 각각이 그 자체로 또는 그것의 보수형태로 모두 존재하는 product이다. - Sum
: 1개 이상의 리터럴들이 OR 연산자로 묶인 것인데, 단 입력변수 X와 그것의 보수 ^X가 동시에 존재하지는 말아야 함.
입력값 X Y Z 3개가 존재하는 로직게이트 L의 출력값은 아래와 같다고 하자.
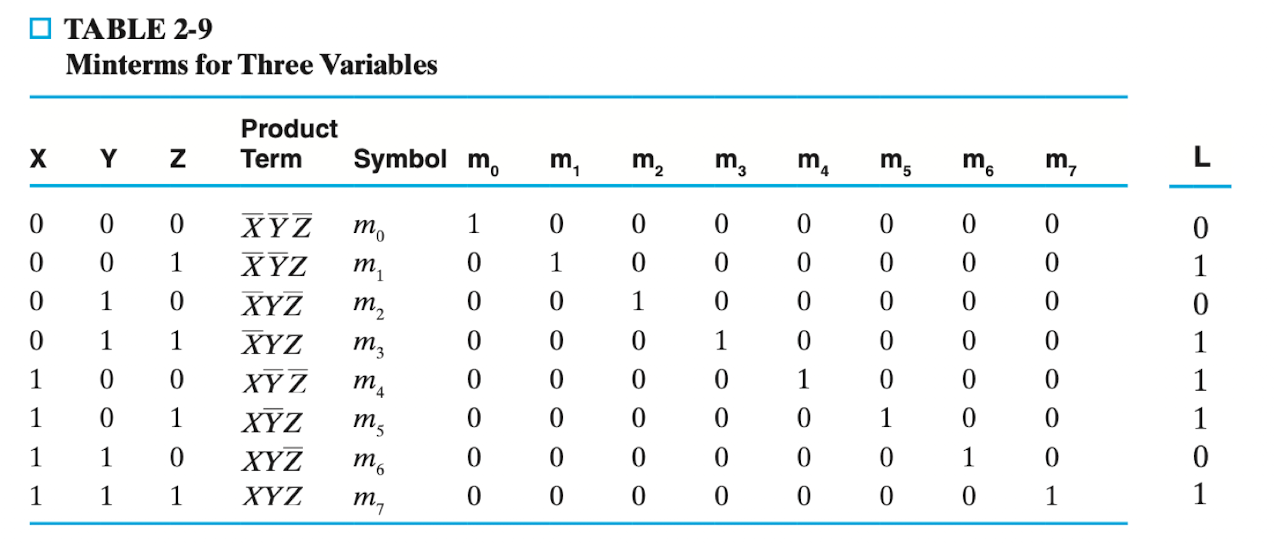
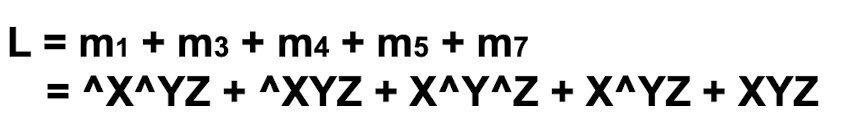
정리하면
논리회로를 표현할 때
- Truth table 진리표 적어 게이트의 특성을 정의하고
- minterm들의 sum으로 부울식으로 표현한다.
- two-level의 로직의 경우 이를 optimize하여, 최소화된 부울식으로 나타낸다.
- 이를 schemetic 으로 그려서 나타낼 수 있다.
Logic Optimization
최소화 되기전의 부울식을 Sum of Minterms 라고 하고,
최소화 된 부울식을 Sum of Products라고 한다.
최소화의 기준
Sum of products로 만들기 위해 optimize할 때,
optimize된 식의 기준을 판단하기 위해 2가지를 보면 된다.
- 첫번째로 Product의 수가 적은지
- 두번째로 literal의 수가 적은지
둘다 같다면 최적화 정도가 같다고 봐도 된다.
예로 아래와 같이 부울식을 조작하여 최소화 할 수 있다.
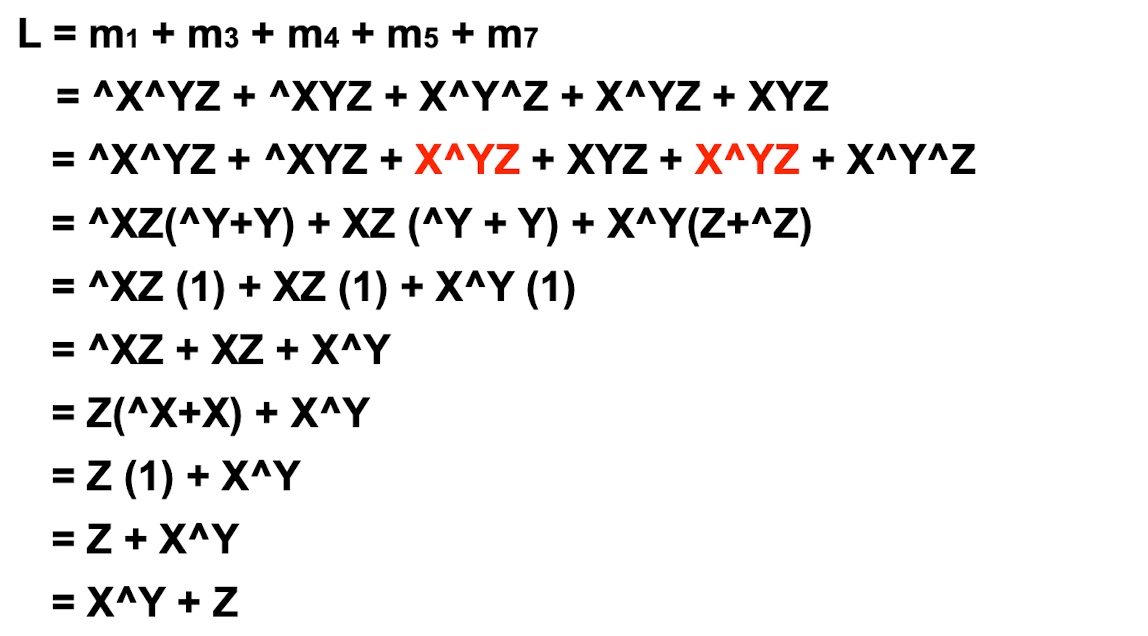
단순법칙 : AB + A^B = A 를 적용하자
[Logic Design - 2]에 계속↗
'Computer Science > Logic Circuit Design' 카테고리의 다른 글
| 논리회로설계 [6] Iterative Circuits (0) | 2022.04.10 |
|---|---|
| 논리회로설계 [5] Encoder & Multiflexer (2) | 2022.04.10 |
| 논리회로설계 [4] Decoder & Adder (0) | 2022.04.10 |
| 논리회로설계 [3] Optimization Algorithm (0) | 2022.04.10 |
| 논리회로설계 [2] K-map with Minterm & Maxterm (0) | 2022.04.10 |

