
본 포스팅은 Logic and Computer Design Fundementals (Pearson, 2013)의 내용을 다루고 있습니다.
Iterative Circuit
Iterative Circuit이란?
동일회로가 반복적으로 연결되어 있는 형태의 회로를 뜻한다.

위 회로를 보면 Cell 회로 n개가 연속적으로 연결되어 있는 상태이므로 iterative 회로라고 할 수 있다.
Half Adder
Half Adder (반가산기)란
두 입력을 더한 값을 binary(2bit)로 출력하는 회로이다.
0, 1, 2, 3 총 4가지 경우에 대한 출력을 가진다.
진리표를 그려 스키메틱으로 나타내면 아래와 같다.
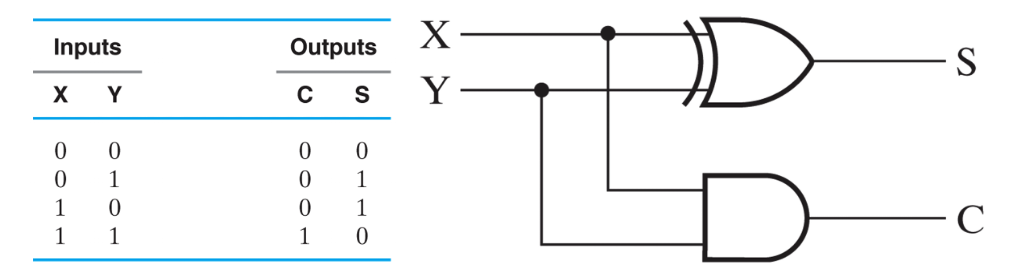
Half Adder
이름이 반가산기인 이유는 올림수(carry)를 생각하지 않는 구조이기 때문이다.
멀티비트의 경우, 더하는 비트의 밑의 자리수에서 carry가 발생한다면
1을 더하여 생각해야하기에, Full Adder가 필요하다.
Full Adder
Full Adder(이하 FA) 란
두개의 비트을 더하고, 올림 수까지 고려하는 가산기이다.
더하는 대상인 두 입력 X와 Y 그리고 올림 수 Z 를 모두 더한다.
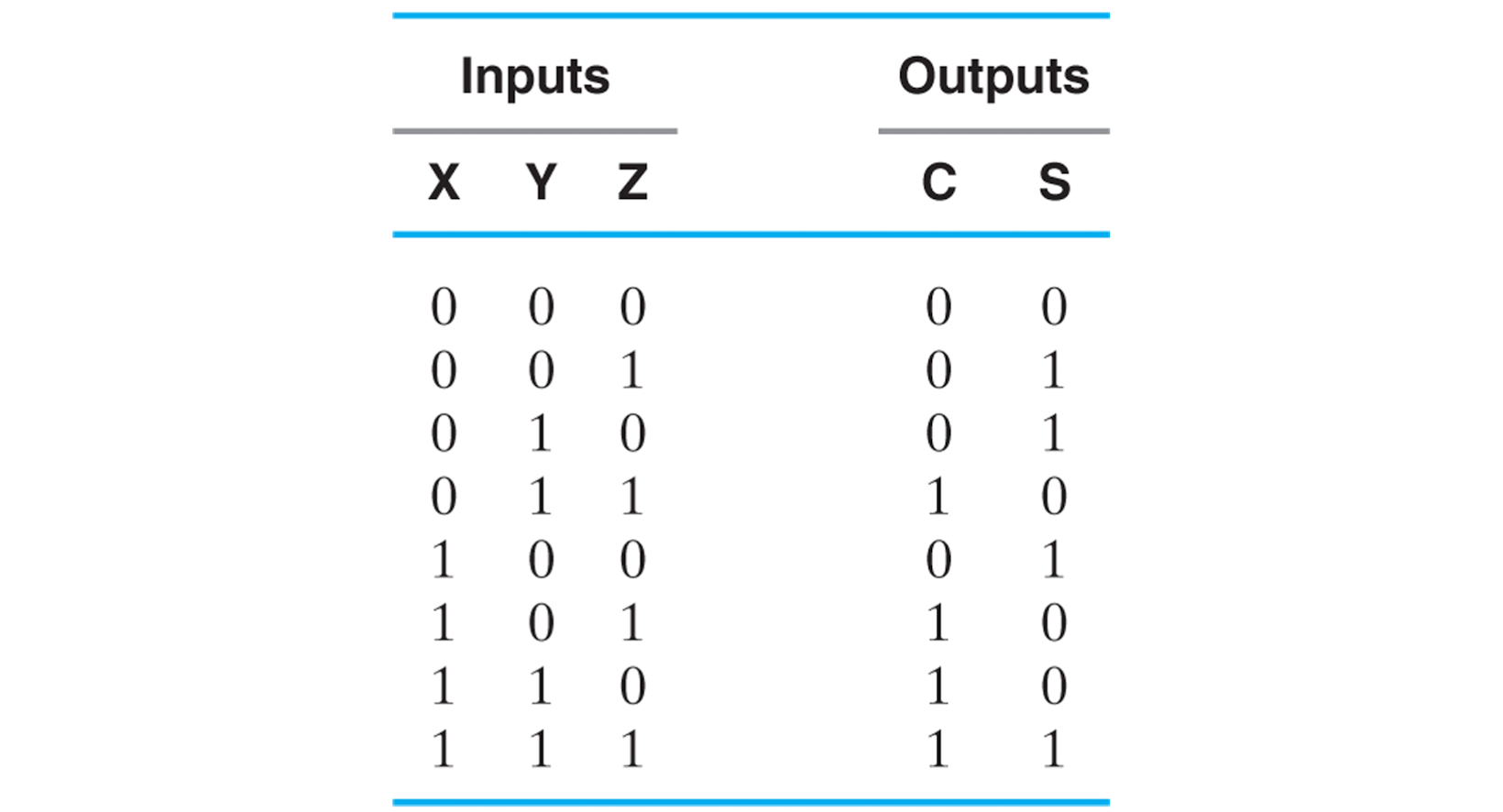
이는 사실 전 포스팅에서 다루었던 1Bit binary adder이다.
전에는 minterm을 OR 연산하는 방법으로 회로를 구현하여 스키메틱을 그렸지만
우리는 그 방법이 최적화 되지 않음을 알고 있다.
sum of minterm들은 K-map으로 나타내어 optimize 할 수 있다.
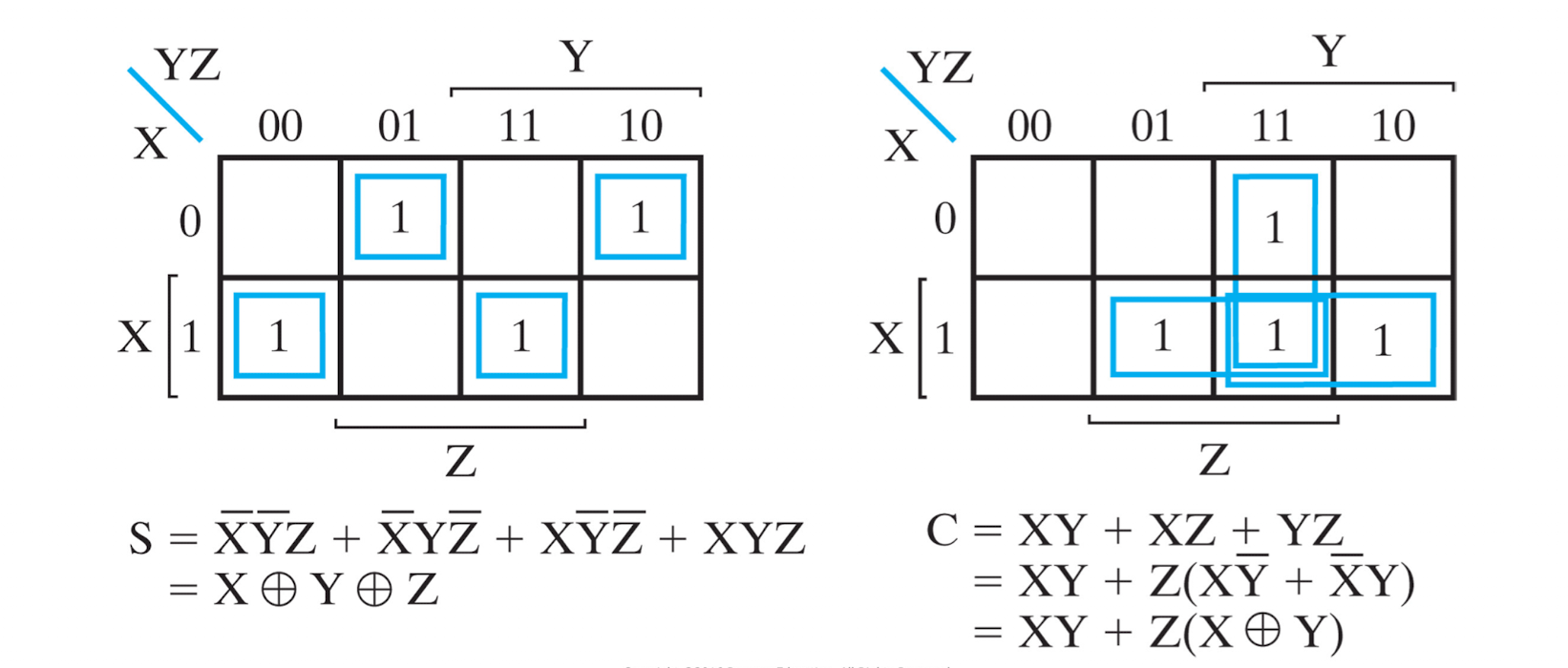
K-map으로 최적화 된 부울식을 위와 같이 구할 수 있고 스키메틱을 그려보면 아래와 같다.

그림을 살펴보면 두개의 반 가산기가 sub-module로서 사용되고 있음을 확인가능하다.
FA도 계층 구조를 가지고 있는 회로이다.
Ripple Carry Adder
Ripple Carry Adder란
여러 개의 Fuller Adder가 반복적으로 연결되어 있는 형태의 회로를 말한다.

Ripple Carry Adder(이하 RCA)는 iterative 회로의 구조를 가진다.
FA에서 올림 수를 고려한다고 하였었는데 RCA에서 이를 활용할 수 있다.
2bit 출력값 C와 S중 높은 자리의 비트인 C를 다음으로 연결된 가산기의 입력(올림)으로 사용하는 것이다.
이런식으로 사용하면 2이상의 멀티 비트를 가지는 두 값 A와 B를 각각의 비트 RCA에 입력하여 합의 비트을 구할 수 있다.
또한, 첫 단계의 FA에서는 올림수가 존재하지 않음이 분명하다.
그러므로 입력값 C0를 그라운드에 연결하여 0을 입력해주거나, FA대신 HA를 사용할 수 있다.
RCA는 장점과 단점을 가지고 있다. - **Pro :** N-bit로의 확장이 매우 용이하다. 마지막 단계의 FA에 FA를 하나더 연결하면 된다. - **Con :** FA를 여러개 연결할 수 록 Logic-Level이 그만큼 증가한다. level이 증가하면 gate delay가 늘어난다.
Adder-Subtractor
뺄셈을 위한 Subtractor를 따로 설계하기 보다는 Adder를 변형시켜 뺄셈도 가능토록 할 수 있다.
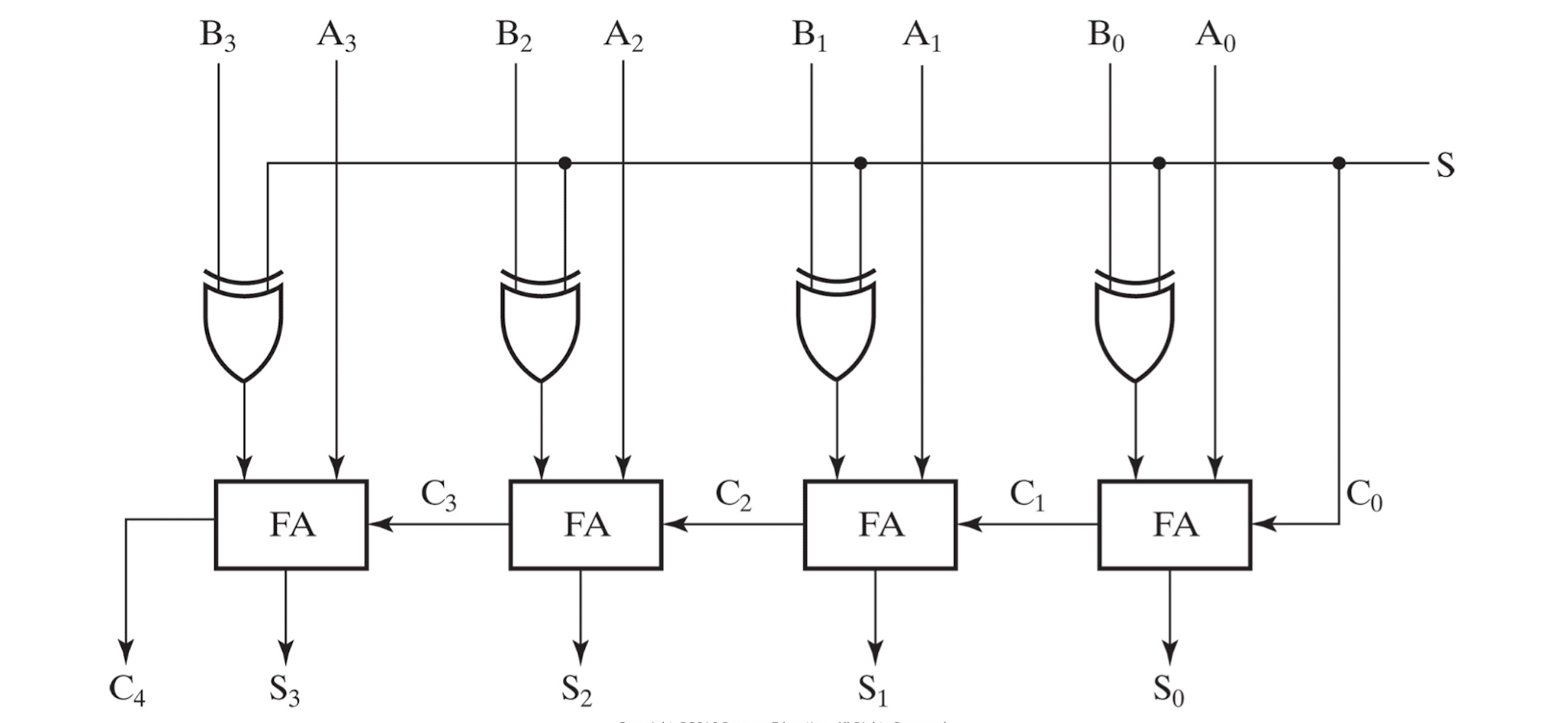
위 회로는 RCA를 변형한 Adder-Subtractor Circuit이며
unsigned 형태의 입력 A - B을 2의 보수 형태로 나타낼 수 있다.
- S가 0인경우
각 B비트 B0 ~ B3는 S와 XOR게이트로 연결되어있다.
S가 0이므로 B는 모두 그대로 출력될 것이며, 첫단계의 FA에 올림수도 0일 것이다.
즉, 정상적인 가산기의 역할 A + B 을 한다.
- S가 1인 경우
XOR게이트에 S 와 연산되는 B 비트들은 S가 1이므로 원 값의 보수가 출력되어 FA의 입력값으로 들어간다.
즉 A + ~B 의 역할을 한다.
이때 첫 단계의 FA에 올림수로 S가 더해지므로, A + ~B + 1 의 연산을 하는 것이다.
~B + 1 는 B 의 2의 보수 형태로, 결국은 A - B 의 연산을 하는 subtractor 로 사용할 수 있다.
다만 마지막 비트의 캐리는 무시한다.
Overflow
주어진 비트내에서 Demical 수를 2의 보수 형태로 나타내다보면 표현할 수 있는 범위를 넘어서는 경우가 있다.
이때 overflow (또는 underflow)가 발생하며, 그 경우 의도하지 않은 값을 얻게될 것이다.
그러므로 adder-subtractor에서 오버플로우가 발생하였는지 알아야 할 필요가 있으므로 추가적인 회로가 필요하다.

마지막과 마지막 바로 전 비트의 FA의 carry를 빼와서 XOR연산하게 되면
오버플로우가 발생했는지 알 수 있는 플래그로 사용할 수 있다.
출력값이 2의 보수 형태로 나타나기에 마지막 비트(MSB)는 signed 비트이다.
그러므로 마지막 비트와, 그 전 비트 둘 중 하나에서만 carry가 발생한다면 오버플로우가 발생한 것이다.
Incrementer
지금 까지는 입력 A 와 B 를 더하거나 빼는 두개의 입력에 대한 연산을 수행하는 회로였다.
Incrementer는 단일 입력 A에 1을 더하주는 회로이다.
물론 이 회로도 Adder를 통해 구현 가능하다.
그냥 입력 B0 의 자리에 1, 그리고 나머지 B 비트의 자리는 그라운드에 연결하면 되기 때문이다.

하지만 단지 1을 더하기 위해 RCA를 사용하기에는 불필요한 게이트들이 많다.
이를 optimize하여 최소한의 필요한 회로를 남겨 설계한다면 Incrementer는 아래와 같다.

Multiplier
곱셈의 연산을 하는 Multiplier도 마찬가지로 RCA를 서브모듈로 가지도록 계층구조로 설계된다.
Multiplier의 구조를 이해하기 위해 다음 비트끼리의 곱셈 연산을 살펴보자

일반 대수 곱셈하듯이 각 비트를 자리수에 맞게 곱하여(AND) 모두 더하면 된다.
위 연산 도출과정의 첫째 줄을 보면 A0 와 B 의 각 비트를 각 자리수에 맞게 AND연산하고 있다.
이는 A0 가 enable 회로의 입력으로서 이용되는 것과 같은 상황이다.
LSB 자리의 연산된 결과인 A0B0 은 더 이상 더할 비트가 없으므로, 그 자리에 바로 출력한다.
그 후, A1 과 AND연산 된 B 비트들을 첫째 줄의 연산결과와 더해준다.

다만, 비트 자리가 다르므로 첫째 줄의 MSB앞에 0을 추가하여 FA로 더해주어야 한다.
이 과정을 반복하는 과정을 회로로 설계하면 Multiplier가 되는것이다.
스키메틱으로 표현하면 아래와 같다.

A 비트들은 Enable 회로의 입력으로 생각하고, 각 자리에 맞게 곱해진 연산결과들을 비트 자리에 맞게 FA로 더해주는 식이다.
Shift 연산
두 입력을 곱하는것이 아닌 단항 입력에 2의 배수를 곱하거나, 나누는 경우에는
multiplier를 곱하는 것 보다는 Shift를 하는것이 더 비용이 적게 든다.
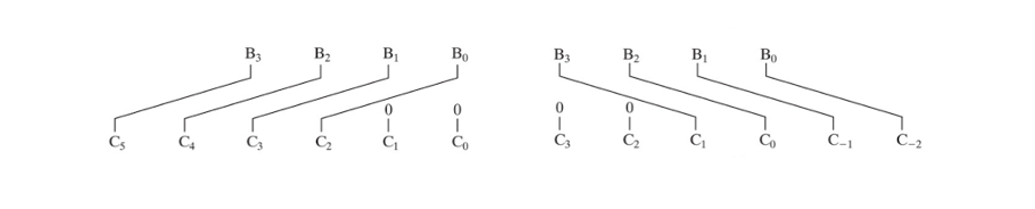
입력 B (4bit) 에 2의 n승을 곱한다면
n 자리 만큼 우측 또는 좌측으로 비트 자리수를 옮긴다.
빈 자리는 0으로 채우면 된다. (Logical)
[Logic Design - 7]에 계속↗
'Computer Science > Logic Circuit Design' 카테고리의 다른 글
| 논리회로설계 [8] FSM & State Assignment (0) | 2022.04.10 |
|---|---|
| 논리회로설계 [7] Latch & Flip-Flop (0) | 2022.04.10 |
| 논리회로설계 [5] Encoder & Multiflexer (2) | 2022.04.10 |
| 논리회로설계 [4] Decoder & Adder (0) | 2022.04.10 |
| 논리회로설계 [3] Optimization Algorithm (0) | 2022.04.10 |

