
본 포스팅은 McGraw-Hill Education의 Data Communications and Networking, 5th Edition By Behrouz .A Forouzan 을 참고하였습니다.
.
3.5 데이터 전송률의 한계
데이터 통신에서 채널을 통해 매초 몇 비트의 데이터를 얼마나 빨리 전송할 수 있는지는 아주 중요한 문제이다. 이러한 데이터 전송률은 3가지 요소에 의해 좌우된다.
- 가용 대용폭
- 사용 가능한 레벨의 갯수(준위)
- 채널의 품짐(잡음의 정도)
데이터 전송률을 계산하는 법은 2가지가 존재한다.
- 잡음이 없는 채널에서 → Nyquist 나이퀴스트 수식
- 잡음이 있는 채널에서 → Shannon 섀넌 수식
3.5.1 무잡음(Noiseless) 채널 : 나이퀴스트 비트율
잡음이 없는 채널의 경우 나이퀴스트 비트율이 이론적인 최대 전송률을 정의한다.

이 수식에서
- bandwidth은 채널의 대역폭
- L은 데이터를 나타내는데 필요한 신호 레벨
- Bit Rate는 매 초당 비트 수
단순히 신호의 레벨을 늘리면 이론적으로 비트율이 올라가지만, 실제로는 신호 구별을 위해 드는 비용으로 시스템의 신뢰도가 떨어질 수 있다.
3.5.2 잡음 채널 : 섀넌 용량 (Shannon Capacity)
현실세계에서는, 사실 잡음이 존재하지 않는 채널이란 존재하지 않는다. 모든 채널은 항상 잡음이 조금이라도 존재하며, 이 때의 최대 전송률을 결정하는 수식이 섀넌 용량이다.
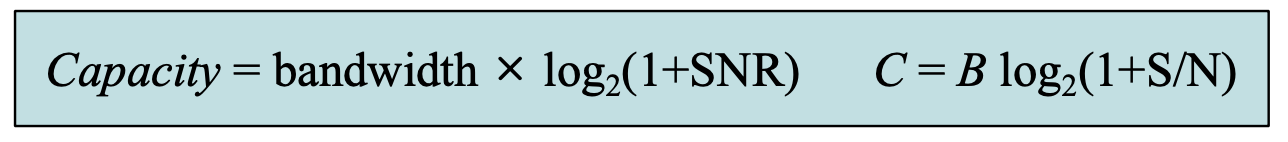
이 수식에서
- bandwidth은 채널의 대역폭
- SNR은 신호에 대한 잡음 비율
- capacity는 bps 단위의 채널 용량 (섀넌 용량)
SNR은 이전 포스팅에서 언급하였듯이 잡음 전력에 대한 신호전력의 통계적 비율이다. 이를 신호-대-잡음 비 SNR이라고 한다.
이 수식에서 주목할만한 점은 수식의 변수에 신호 레벨이 들어가지 않는다는 것이다. 이는 레벨의 수를 아무리 늘려도 일정 한계 이상의 전송률을 달성할 수 없음을 알 수 있다.
섀넌 용량은 채널의 특성을 정의하는 것이지, 전송 방법을 정의하는 것이 아니다.
3.5.3 두 가지 방법을 함께 사용
현실 세계에서는 어떤 신호 레벨과 어떤 대역폭이 필요한지 알기 위해 두 가지 방법을 모두 사용하여 구한다.
예를 들어 1MHz의 bandwidth을 갖는 채널이 있고 SNR이 63이라고 하자. 이때의 bitrate와 level을 구해보자.

먼저 잡음이 있는 채널의 상한을 구하기 위해 섀넌 용량을 사용한다. 6Mbps이 이 채널의 상한이다. 하지만 더 좋은 성능을 위해 조금 더 낮은 값은 4Mbps로 정한다고 치자.
그 후 이제 나이퀴스트 정리로 신호 레벨(준위)를 구할 수 있다. 위 식에서 4 단계로 준위로 채널 신호를 구성하면 됨을 알 수 있다.
- Shannon 용량은 전송률의 상한 값을 알려준다
- Nyquist 공식은 몇 개의 신호 레벨이 필요한지 알려준다

