
본 포스팅은 McGraw-Hill Education의 Data Communications and Networking, 5th Edition By Behrouz .A Forouzan 을 참고하였습니다.
.
4.1 디지털 대 디지털 변환
4.1.1 회선 부호화 (Line Coding)

회선 부호화는 디지털 데이터를 디지털 신호로 바꾸는 작업이다. 예를 들면 문자, 숫자, 이미지, 영상과 같은 비트의 연속인 데이터를 디지털 신호로 부호화 하고, 수신자가 이를 복호화 하여 디지털 데이터를 재생하게 된다.
회선 부호화의 몇 가지 특성
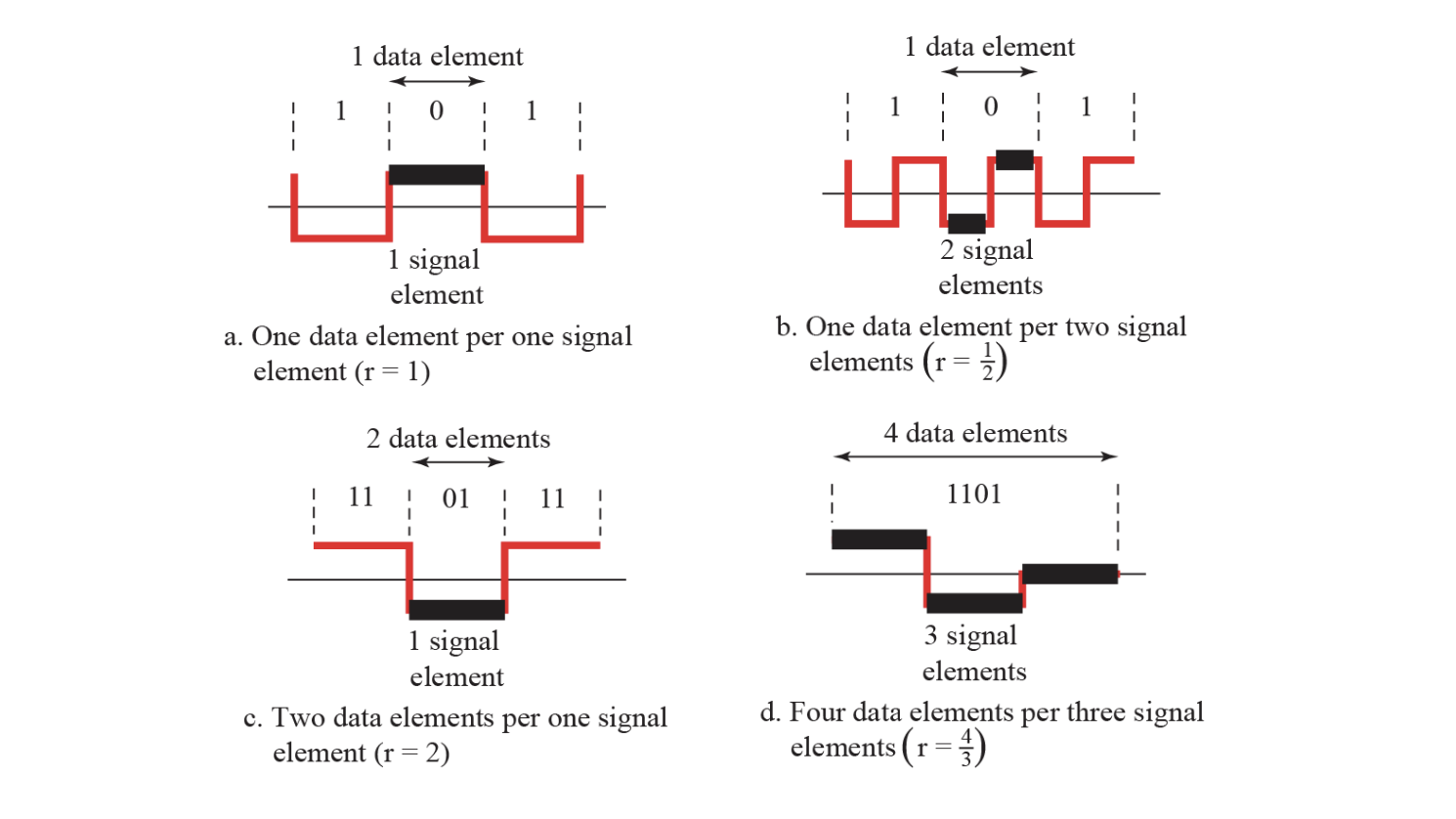
- 신호요소 vs 데이터 요소
- 데이터 요소란 정보를 표현하는 가장 작은 개체로 비트를 사용
- 신호요소가 데이터 요소를 전달
- 신호요소란 시간적으로 볼 때 디지털 신호의 가장 짧은 단위
- 데이터 요소는 우리가 전달해야 하는 것, 신호 요소는 전달자

- 데이터 전송률 대 신호 전송률
- 데이터 전송률은 1초당 전송된 데이터 요소의 개수 (bps)
- 신호 전송률은 1초당 전송된 신호 요소의 개수 (baud)
- 신호 전송률 a.k.a. 보오율, 펄스율, 변조율
- 신호 전송률을 낮추고 데이터 전송률을 높혀야 한다
- 신호 전송률 = 데이터율 / 한 신호요소가 싣는 데이터 요소의 갯수
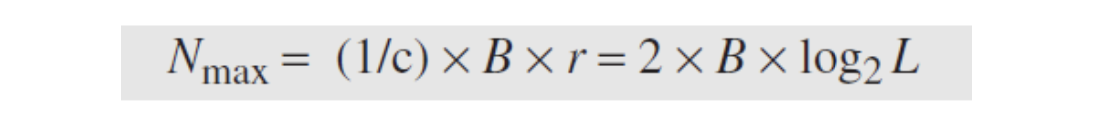
- 대역폭
- 대역폭은 이론적으로 무제한이지만 대부분은 한정된 대역폭을 가짐
- 실제 디지털 신호의 대역폭은 무한, 유효대역폭은 유한하다
- 비트율이 아닌 신호 전송률(보오율)이 요구 대역폭을 결정한다
- 최대 데이터률 = 대역폭 x 한 신호요소가 싣는 데이터 요소의 갯수
- 나이퀴스트 정리에 의하면
N = 2 * B * r
그외로
- 기준선 표류
- 직류성분
- 자기 동기화
- 내장형 오류 발견
- 잡음과 간섭신호에 대한 내성
- 복잡도
등의 특성을 가진다...
4.1.2 회선 부호화 방식
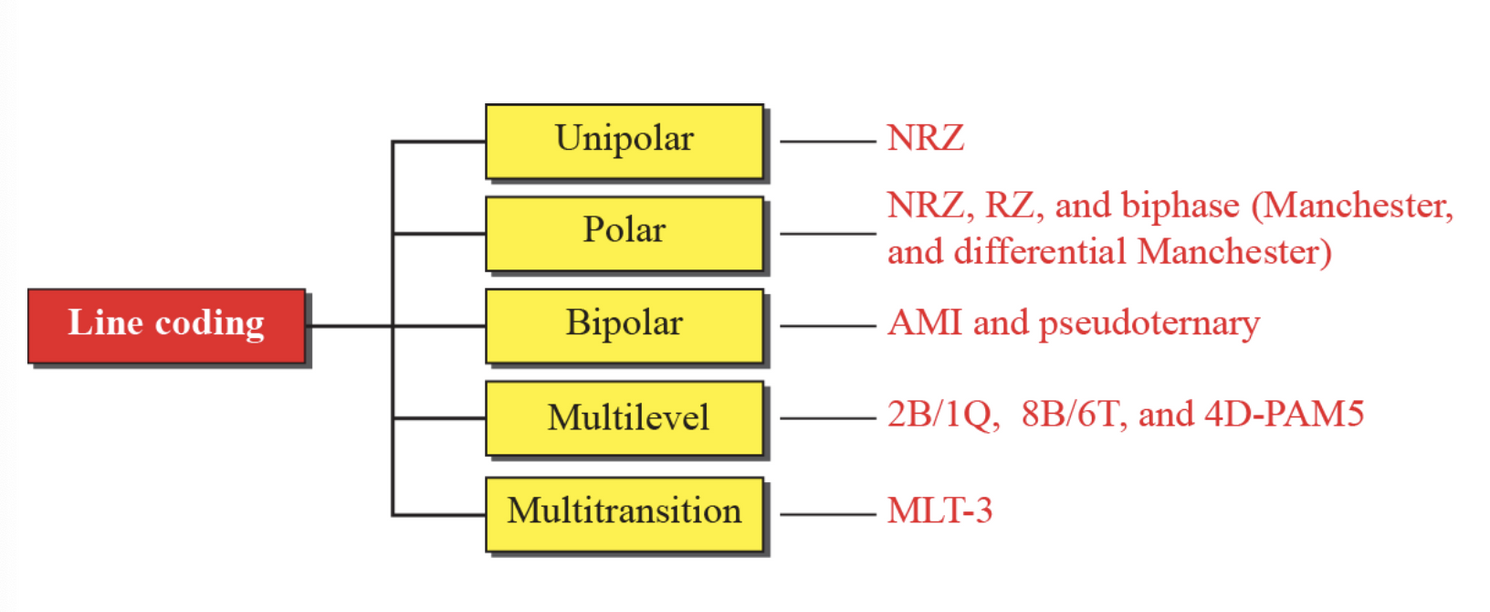
회선 부호화의 방식은 위 그림과 같이 5가지로 나눌 수 있다.
단극형 (Unipolar Schemes)
단극형 부호화는 시간 축을 기준으로 전부 위 또는 아래 신호 레벨의 값만 사용한다.
단극형 NRZ 영비복귀
단극형 부호화는 주로 영비복귀 (NRZ, non-return-to-zero) 방식으로 설계되었다.
- 양 전압은 비트 1
- 음 전압은 비트 0
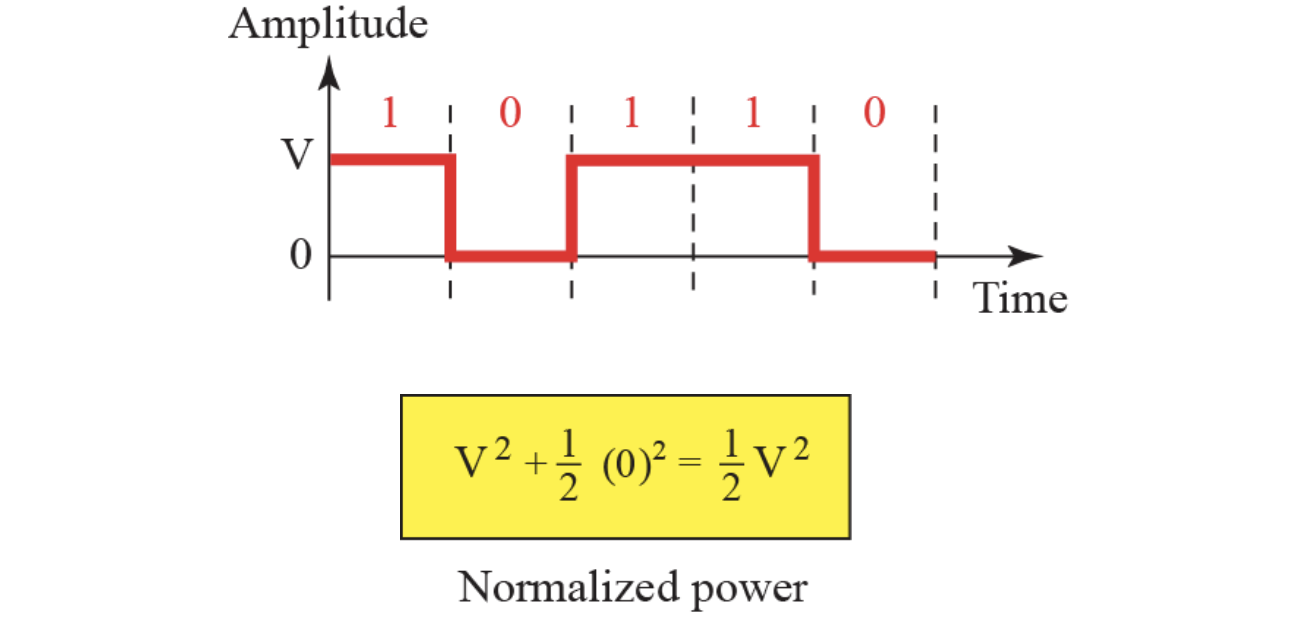
이 방법은 매우 소모적이다. 이는 정규화된 전력이 극형 NRZ에 비해 두 배로 비효율적이여서 오늘날에는 거의 사용되지 않는다.
Polar 극형
극형 부호화에서 전압은 시간 축의 양측을 사용한다.
예를 들면 0에 대한 전압 레벨은 양을 사용 하고 1에 대한 전압 레벨은 음을 사용한다.
극형 NRZ 영비복귀
극형 영비복귀 부호화에서는 두 가지 레벨의 신호를 사용한다.
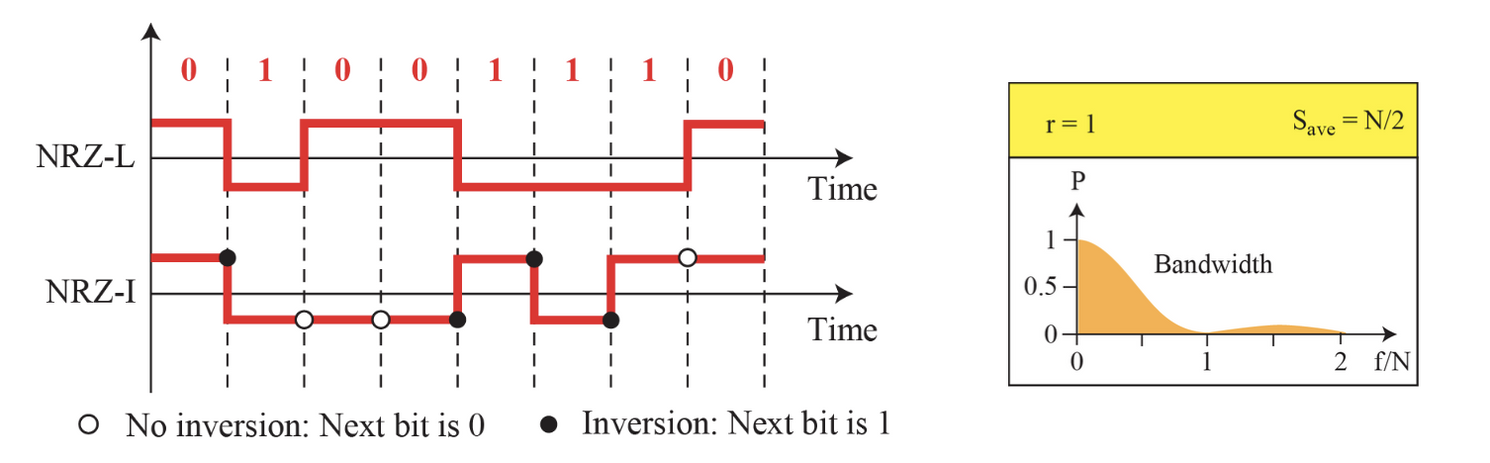
- NRZ-L (level)
- 전압 준위가 비트의 값을 결정한다
- 연속적으로 같은 값이 들어오면 평균 신호 전력이 일그러지는 기준선의 표류 문제 발생
- NRZ-I (Invert)
- 전압에 변화가 있거나 없는 것으로 비트의 값을 결정한다
- 전압 변화가 없으면 0, 바뀌면 1이다.
- 0 이 계속 들어오면 기준선의 표류 문제 발생
두 방법 모두 평균적인 신호 처리율은 N/2 baud 이다. 두 방법 다 기준선의 표류와 동기화 문제를 가지고 있다. 또한 에너지가 골고루 분산되어 있지 않은 직류성분의 문제가 있다.
극형 RZ 영복귀
NRZ의 주 문제는 송신자와 수신자가 동기화 되지 않을 떄 생기게 된다. 수신자는 언제 비트가 종료되고 언제 다음 비트가 시작되는지 명확하게 알 수 없다. 이러한 문제를 해결하기 위해 RZ 영복귀 방법을 사용할 수 있다.
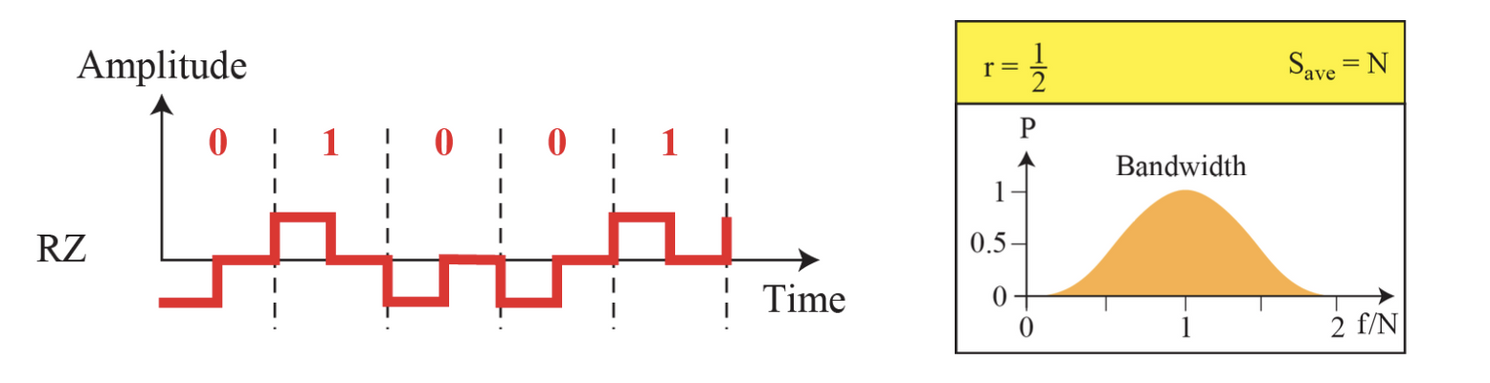
RZ 영복귀 신호는 비트와 비트 사이에서만 바뀌지 않고 매 비트 구간동안에 0으로 돌아온다. 그러면 비트이 시작과 끝을 0으로 명확하게 구분할 수 있다.
다만 한 비트를 부호화하기위해 두 번의 신호 변화가 필요하므로 너무 많은 대역폭을 차지하게 된다. 또한 3개의 준위(레벨)을 사용하므로 구별하는 것이 복잡하다. 이러한 이유로 극형 RZ 또한 오늘날 사용하지 않는다.
Biphase 양위상
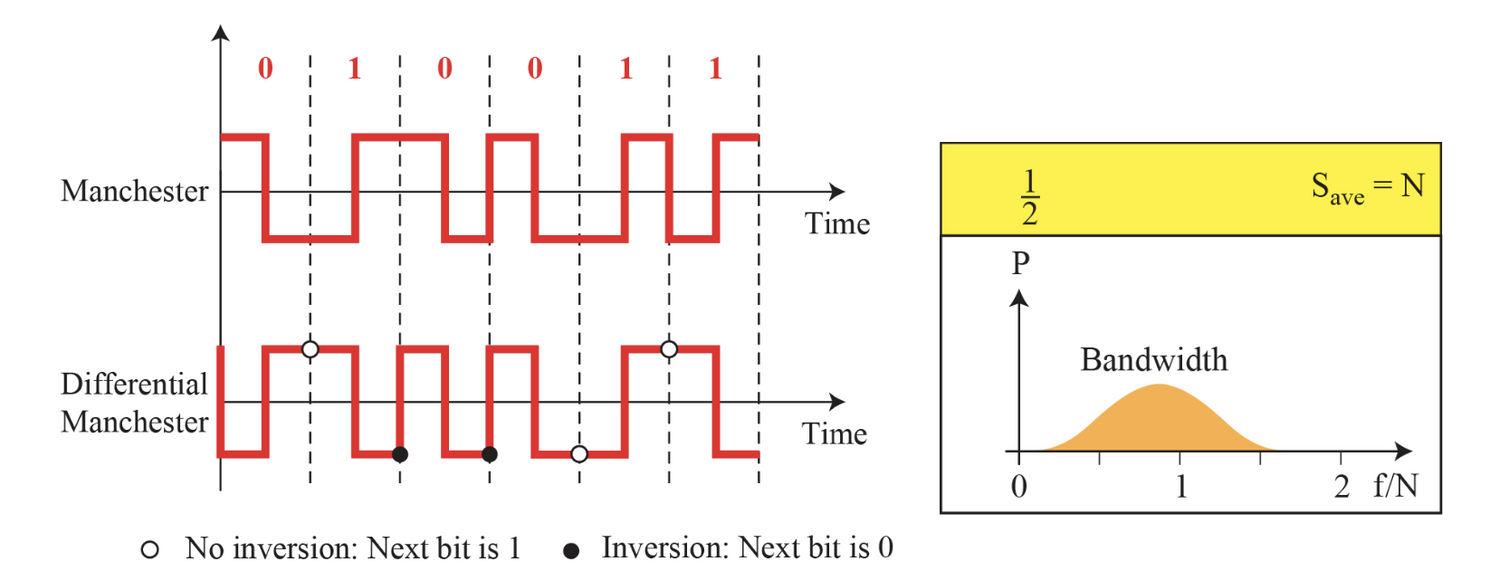
- Manchester 맨체스터
- RZ의 아이디어와 NRZ-L의 아이디어를 섞음
- 비트 중간의 전이가 양→음 이면 0
- 비트 중간의 전이가 음→양 이면 1
- 동기화와 비트 판별을 동시에 할 수 있다
- Differential Manchester 차분 맨체스터
- RZ의 아이디어와 NRZ-I의 아이디어를 섞음
- 비트 중간의 전이는 동기화를 위해 항상 전이
- 비트 간격 점에서 전이 여부로 비트 판별
- 전이가 있으면 0, 전이가 없으면 1
맨체스터 방식은 NRZ의 몇가지 문제를 해소한다.
- 기준선 표류의 문제
- 직류 성분을 제거 → 양과 음의 전압이 고름
유일한 단점은 NRZ에 비해 신호율이 2배로 높다는 것이다. 각 비트의 중간마다 항상 전이가 일어나며 간격 사이에도 일어날 수 있기 때문이다.
Bipolar 양극형
때로는 다준위 2진수라고 불라는 양극형은 양, 음, 영의 세가지 전압 레벨을 사용한다.
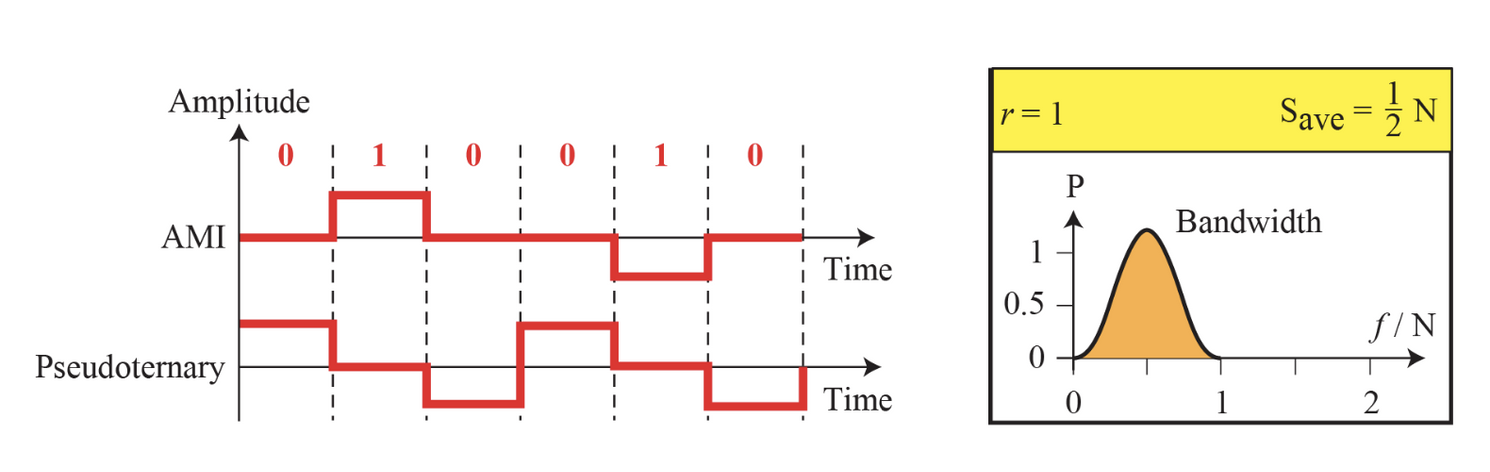
- AMI(Alternate Mark Inversion) 교대 표시 반전
- pseudoternary 가삼진수
등의 방법이 존재하며 직류 성분이 없다
Multilevel 다준위
m 비트와 n 레벨을 가진다. 2진수의 경우 B(binary) , 3진수의 경우 T(teneary), 4진수의 경우 Q(quaternary)
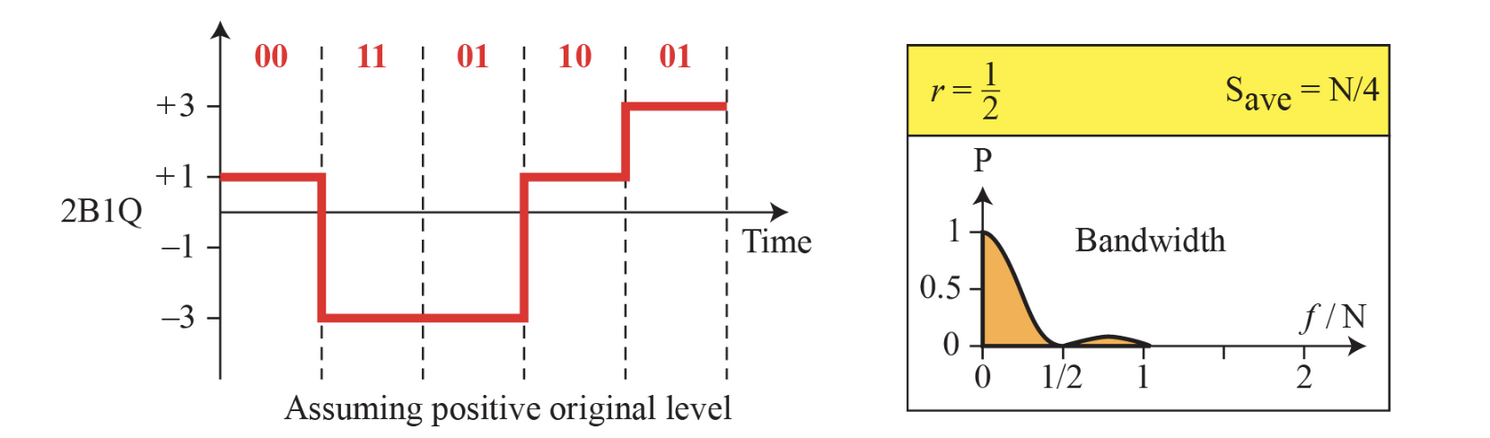
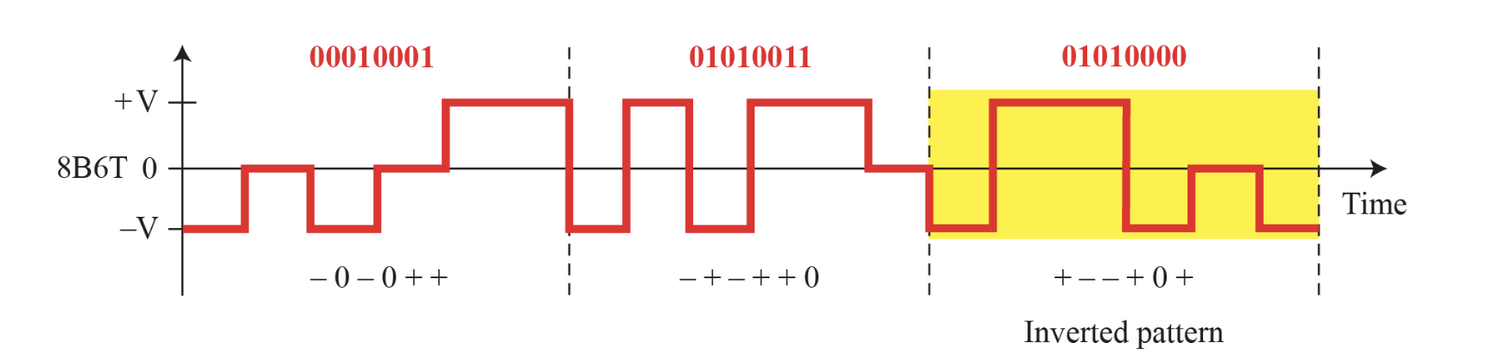
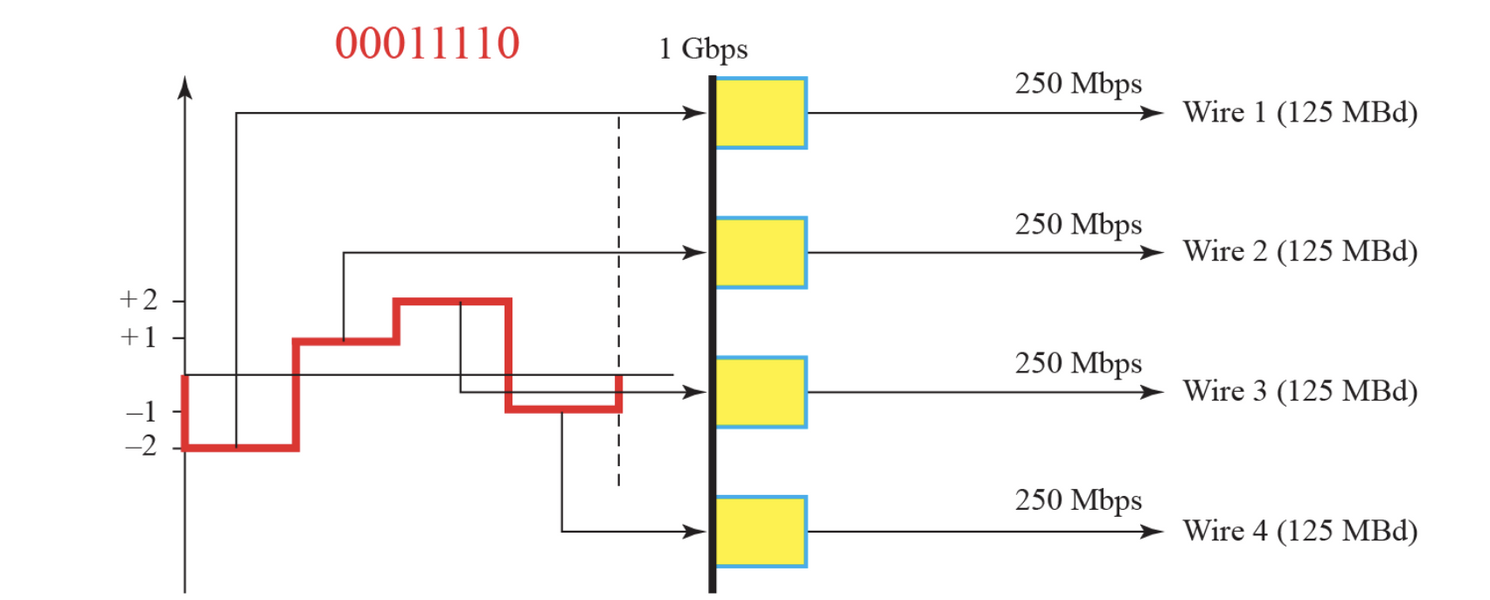
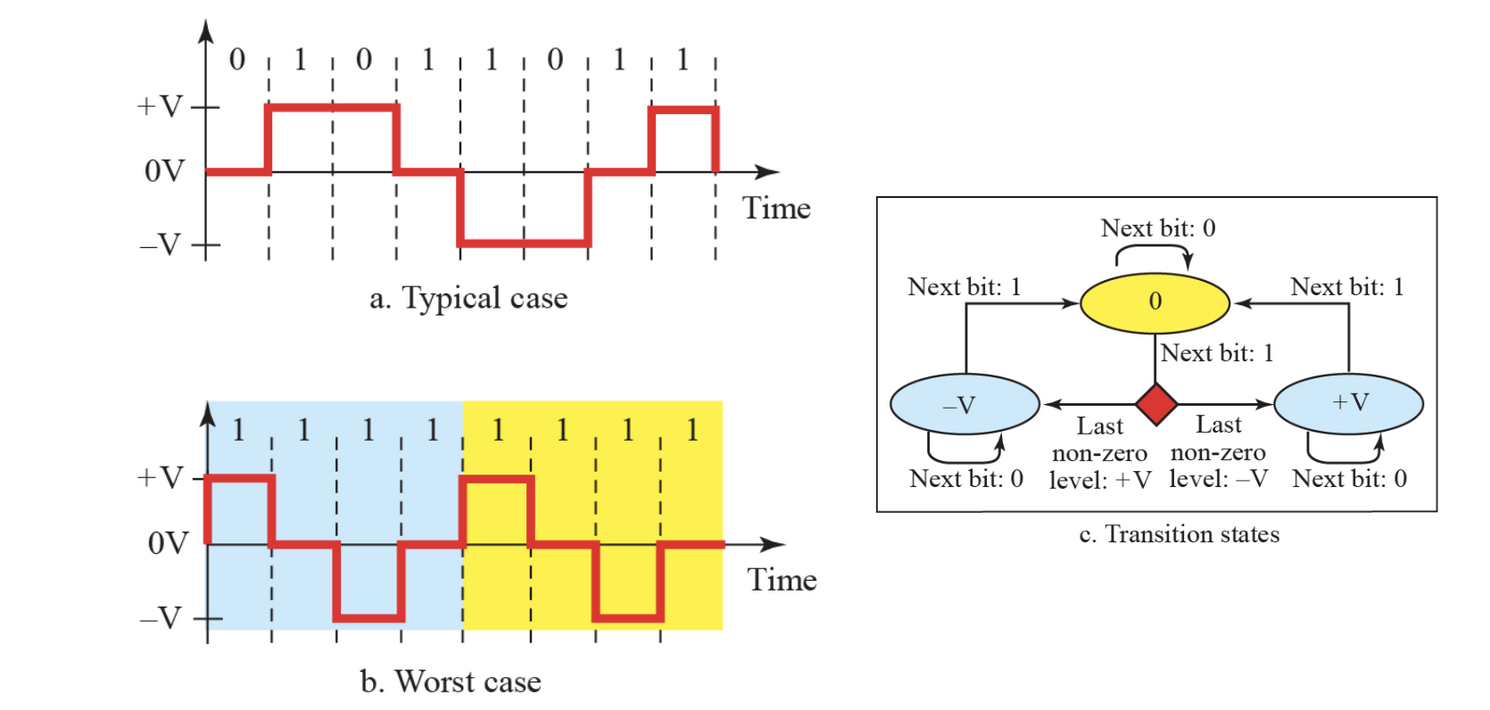
자세한 설명은... 너무 많아서 설명하겠습니다. 직접 찾아보세요~~
요약
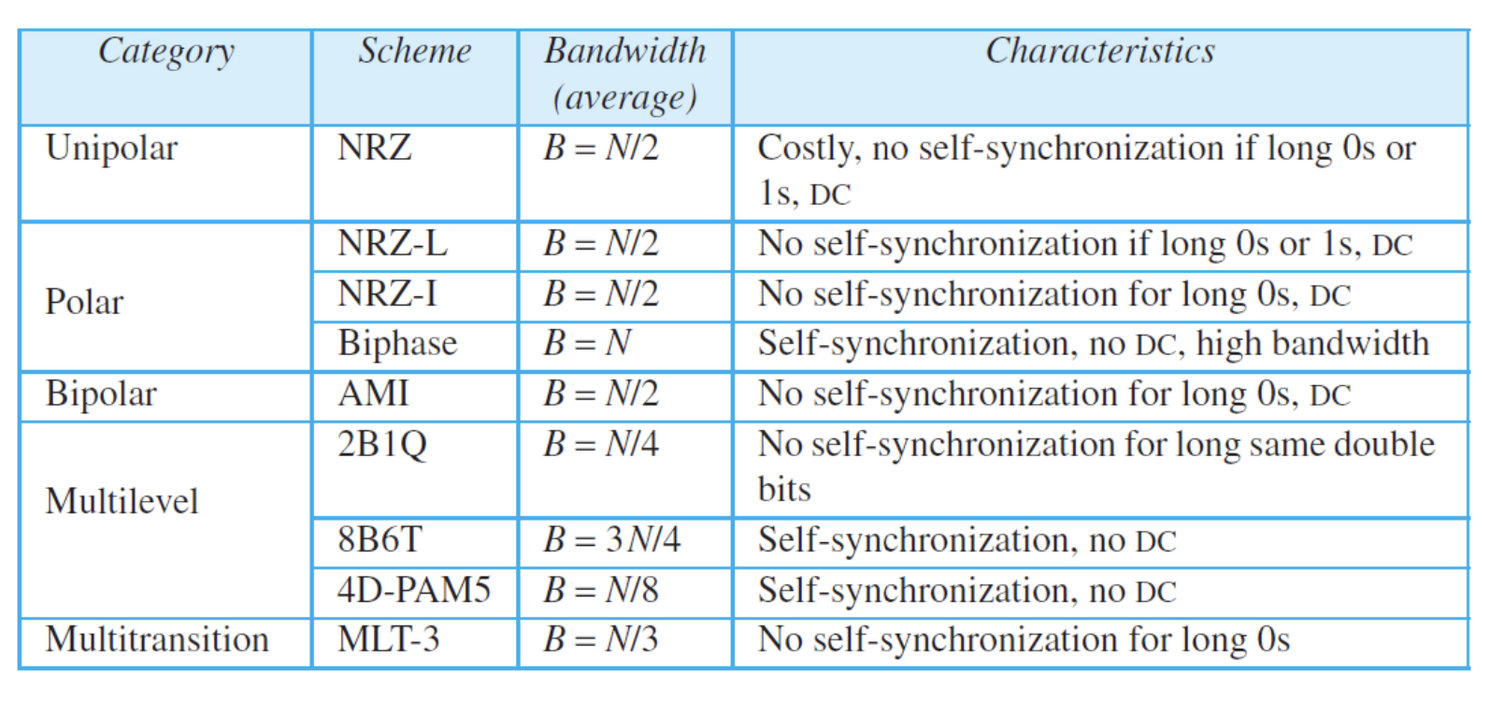
4.1.3 블록 부호화

동기화를 확보하기 위해서는 어떤 식이든 여분의 비트가 필요하다. 더욱 이 오류를 검출하기 위해서도 다른 여분의 비트를 포함시키지 위해 블록 부호화를 사용한다.
블록 부호화는 m 개의 비트를 n 개의 비트 블록으로 바꾸는데 여기서 n은 m보다 작다. 블록 부호화는 mB/nB 로 표기하기도 한다.
4B/5B
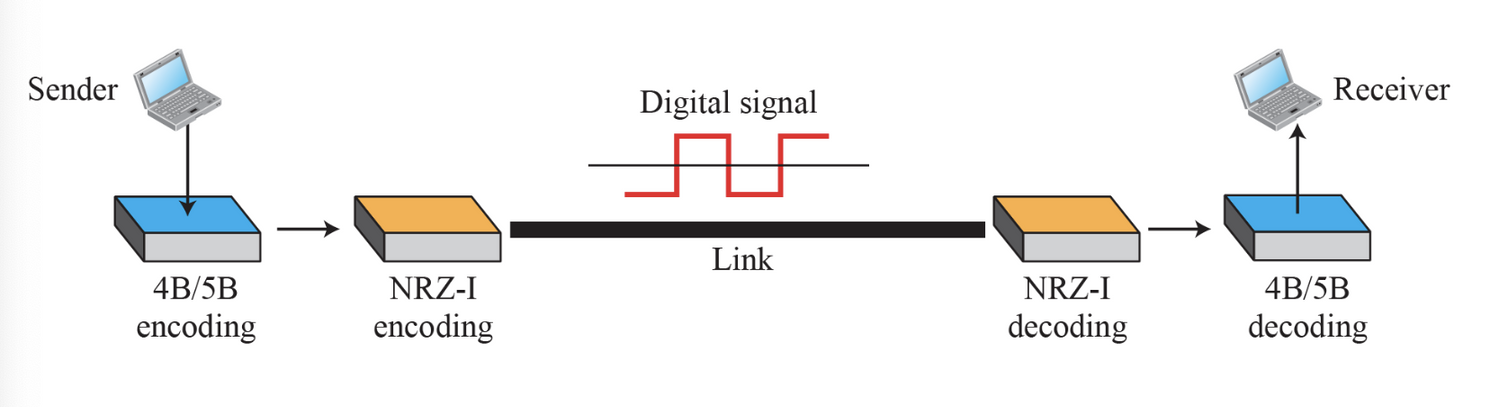
4B/5B 부호화는 NRZ-I 와 혼합하여 사용하기 위해 고안되었다. 앞서 말했듯이 NRZ-I 방식은 좋은 신호율을 가지지만 연속되는 긴 0은 전이가 일어나지 않게 하고 동기화를 잃어 버리게 된다.
이에 NRZ-I 로 변환하기 전에 연속되는 0이 생기지 않도록 스트림을 바꾸면된다. 4개의 비트를 5개로 바꾸는데, 각 코드는
- 1개보다 많은 0으로 시작하지 않고
- 2개보다 많은 0으로 끝나지 않는다
즉 5개의 비트 코드는 절대 3개보다 많은 0이 연속되지 않는다.
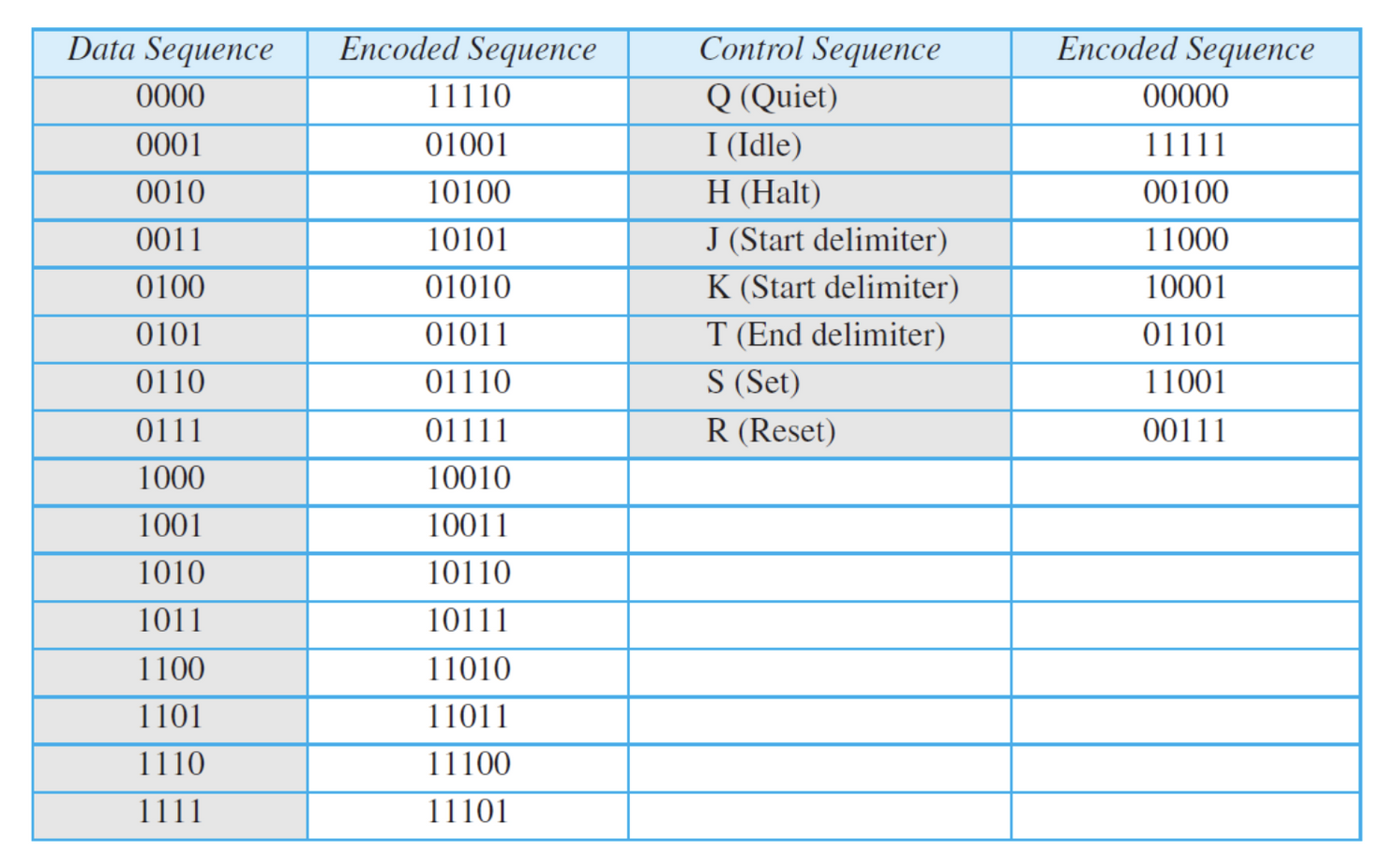
4개의 비트를 바꾸는 기준은 위 표와 같은 mapping table을 따른다.
만약 수신자는 부호화된 블록에 해당하지 않는 비트셋을 받게 되면 오류를 검출할 수 있게 된다.
4B/5B 부호화는 동기화 문제를 해소하여 NRZ-I의 한가지 문제점을 해결하지만 추가적인 여분의 비트를 추가함으로써 신호율을 증가시킨다. 그래도 +20% 로 NRZ의 2배를 사용하는 Biphase보다는 적은 값이다.
그래도 여전히 블록 부호화는 직류 성분 문제를 해결하지 못한다.
8B/10B

8비트 셋이 10비트 셋으로 바뀌는 것을 제외하면 4B/5B 부호화와 유사하다. 일반적으로 더 나은 오류 확인 기능과 향상된 동기화 때문에 더 우수하다고 한다.

